Strukture podataka i algoritmi 1
SPA1 - Vežbe 4
Rekurzija
Rekurzija je koncept gde funkcija poziva istu takvu funkciju, samo sa drugačijim parametrima. Ovo omogućava rešavanje problema tako što se problem deli na manje instance istog problema, koje se zatim rešavaju rekurzivnim pozivima funkcije.
Kada se funkcija poziva, prvo se proverava uslov zaustavljanja ili bazni slučaj, koji predstavlja kraj rekurzije. Ako je uslov ispunjen, funkcija se zaustavlja i vraća rezultat. Ako uslov nije ispunjen, funkcija izvršava rekurzivni poziv, koji deli problem na manje instance istog problema. Rezultati tih manjih instanci se zatim kombinuju kako bi se dobio konačan rezultat.
Rekurzija se može koristiti za rešavanje različitih problema, kao što su izračunavanje faktorijela, Fibonačijev niz, pretraga stabla, sortiranje, i mnogi drugi. Međutim, važno je voditi računa o efikasnosti rekurzivnih rešenja, jer neefikasna rekurzija može dovesti do prevelikog broja rekurzivnih poziva i potencijalno do prekoračenja steka (stack overflow). Ukoliko je problem moguće rešiti iterativno, najčešće je bolje rešiti ga tako da ne bi došlo do prekoračenja steka.
Rekurzija je moćan alat za rešavanje određenih problema u programiranju, ali se mora koristiti sa oprezom i razumevanjem kako bi se izbegli potencijalni problemi sa performansama i upravljanjem memorijom.
Poređenje rekurzivnog i iterativnog pristupa
Prednosti
| Rekurzivni pristup | Iterativni pristup |
|---|---|
| Jednostavnost implementacije (i najčešće kraći kod) kod određenih problema. | Efikasnost: Može biti brži i zahtevati manje memorije u nekim slučajevima. |
| Prirodnost kod rešavanja određenih problema (npr. strukture podataka kao što su binarna stabla). | Manja verovatnoća prekoračenja steka za duboke rekurzivne pozive. |
| Jasnoća i elegancija koda kod problema koji prirodno koriste rekurziju. | Lakše razumevanje kod manje složenih problema. |
| Fleksibilnost: Rekurzivni pristup može biti koristan kada je potrebno rešiti problem koji se može lako podeliti na manje instance istog problema. | Mogućnost optimizacije kroz upotrebu petlji i smanjenje memorijskog opterećenja. |
Mane
| Rekurzivni pristup | Iterativni pristup |
|---|---|
| Moguće prekoračenje steka za duboke rekurzivne pozive, što može dovesti do pada performansi i potencijalnog rušenja programa. | Složenost: Kod nekih problema, iterativno rešenje može biti manje intuitivno i složenije za implementaciju. |
| Potencijalno veće memorijsko opterećenje zbog dodatnog prostora na steku za svaki rekurzivni poziv. | Manje prirodno za neke probleme koji se prirodno rešavaju rekurzivno. |
| Potreba za baznim slučajem ili uslovom zaustavljanja kako bi se sprečila beskonačna rekurzija. | Manje efikasan kod nekih problema koji zahtevaju ponavljanje velikog broja koraka. |
Primeri
1. Faktorijel
Definicija: n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1
Kod:
int factorial(int n) {
if(n == 0 || n == 1) { // bazni slučaj za koji nije potrebno računanje i čiju vrednost znamo
return 1;
}
return n * factorial(n-1); // rekurzivni poziv
}
Ilustracija steka prilikom izvršavanja funkcije:
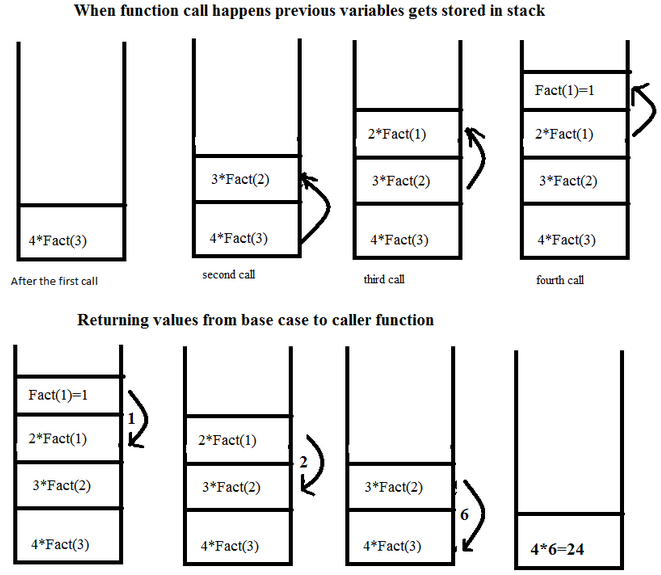
2. Stepen celog broja sa pozitivnim eksponentom
Definicija: а ^ b = a * a * a * ... * a (ukupno b puta)
Kod:
int stepen(int a, int b) {
if(b == 0) { // bazni slučaj za koji nije potrebno računanje i čiju vrednost znamo
return 1;
}
return a * stepen(a, b - 1); // rekurzivni poziv
}
Zadaci za vežbu
Rešiti rekurzivno sledeće probleme:
- Suma svih članova niza
- Minimum niza
- Maksimum niza
- Prosek niza
- izračunavanje n-tog člana Fibonačijevog niza
- pretvaranje prirodnog broja iz dekadnog sistema u binarni sistem
- Implementacija funkcije najveći zajednički delilac za brojeve x i y. Prema Euklidovoj teoremi ako su x i y pozitivni celi brojevi takvi da je x >= y, onda je nzd(x, y) = nzd(y, x%y). Posledica teoreme je nzd(x, 0) = x.